朝日新聞から
【要説】
●苦手な子どもが多い分数の計算。それを視覚的に理解しようと、浜松市内の小学生=当時=が「分数ものさし」を考えた
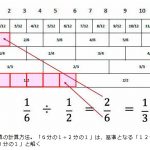
●長さ12センチのものさしに5列の目盛りが付き、基準単位の「12分の1」がいくつあるか数えて計算する――。この発想に静岡大が注目し、教材化に向けた研究も進む
●小5の時、分数に苦手意識を感じたという。友人も悩んでいた。掛けるのになぜ、答えは小さくなるのか。割り算ではなぜ、割る方の分母と分子を入れ替えて逆数にするのか……
●学習塾の経営に携わる父裕一朗さん(40)にも疑問をぶつけ、やがてものさしで分数を考える発想にたどり着く。1とその数以外では割り切れない「素数」の目盛りだけがついた京都大の「素数ものさし」がヒントになった
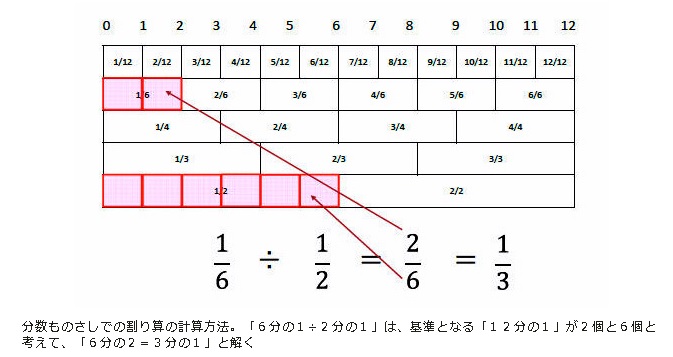
●分数ものさしには、12分の1ずつ刻まれた目盛りに対応して「6分の1」「4分の1」「3分の1」「2分の1」ずつ刻まれた全5列の目盛りが付く。基準となる「12分の1」が何個かを数えて計算する。「4分の3」と「3分の2」、どちらが長いかも分かる
>割り算ではなぜ、割る方の分母と分子を入れ替えて逆数にするのか
◆たしかに分かりにくいですな。
分母が割り算の応用で、割り算は掛け算の入れ違えと覚えれば分かるかも?
ツイッターで九九票が話題になっていたが↓
https://twitter.com/mauzoun/status/847078659336822785
こうして見ると、「分数ものさし」と九九票は似てるのでは?と。
ん?目新しさがないのだが?
今の学校って逆にどうやっておしえてるの?
>「素数ものさし」がヒントになった
というか、素数でそれがやれるってことは、
順序的には元々あったものじゃないのかね?
まぁ1/6の半分が1/3って直感でもわかりそうだが
数学苦手な人って苦手なのに数字を数字と見すぎてる傾向があるように思える
判りやすいか?
余計わかりにくいような気がするんだが
ちなみに1/6の半分は1/12だよ
物理や数学は、リアルの現象を数式に圧縮し、数式からリアルの現象を展開する能力が必要
このものさしは、数式からリアルを展開する考え方の1つだろう
だから、考え方が合わなかったら、そりゃ分かりにくい
この式で何が起きているのか、という発想が先に出て
頭から離れないタイプの人には非常に助かるものなのかもね
俺は単純だから、
「ほーん、分母と分子を入れ替えて掛け算すればええんな?」
でとくに何も考えなかったし、割り算の考え方も今調べて知ったわ
(A÷B=CはAのなかにBがC個ある、という意味だそうで)
そうそう
「なぜそうなるのか」より、「どうすれば答が出るのか」を優先する人はそうなる
「それじゃいかん」「論理的な物の考え方が身につかない」って人もいるだろうけど、数学を道具として使っているうちは、それでいいと思ってる
商が1を超える場合には使えない?
このものさし使わなくてもリンゴとかで普通に説明できるし
逆にこのものさしで理解できるならちゃんと説明聞いてれば理解できるんじゃない?
当時どうやって教えられたのかまで覚えてないが、いままでの教え方がよっぽど悪かったのか?
ぶっちゃけ数学の公式に「これなんでこうなるの?」という疑問を持ってはいけない